超导量子计算导论
本文最后更新于:5 个月前
量子计算简介
Bloch球
量子比特的纯态可以用Bloch球表示
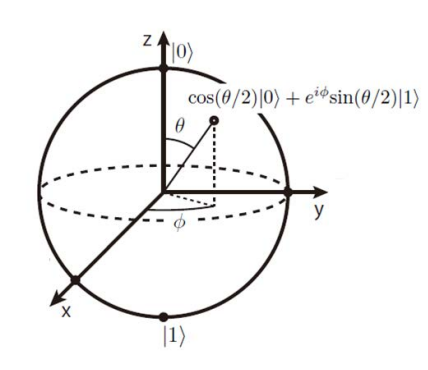
\[ \ket{\psi}=\cos({\theta\over2})\ket{0}+e^{i\phi}\sin({\theta\over2})\ket{1} \] 注意这里的\(\theta\)会和布居数(占据数)联系,\(\phi\)则是相对相位(这很显然)
旋转操作算符
考虑对一个量子态在Bloch球上进行旋转操作,旋转轴为\(\vec{n}\),旋转角度为\(\alpha\) 记为 \[ \hat{U}=\hat{U}(\vec{n}, \alpha)=e^{-i\alpha{\vec{n}\cdot\hat{\vec{S}}\over\hbar}} \] 对于Bloch球表示的体系,\(\hat{\vec{S}}={\hbar\over2}\hat{\vec{\sigma}}\) 所以我们可以得到旋转操作算符 \[ \hat{U}(\vec{n}, \alpha)=e^{-i{\alpha\over2}\vec{n}\cdot\hat{\vec{\sigma}}}=\cos({\alpha\over2})-i\vec{n}\cdot\hat{\vec{\sigma}}\sin({\alpha\over2}) \] 这里已经利用了扩展的欧拉公式,其中\((\vec{n}\cdot\hat{\vec{\sigma}})^2=\hat{I}\) 证明如下 \[ \hat{q}^2=\hat{I} \]
\[ e^{i\theta\hat{q}}=\sum_{k=0}^\infty[{(-1)^k\theta^{2k}\over(2k)!}+i\hat{q}{(-1)^k\theta^{2k+1}\over(2k+1)!}] =\cos\theta+i\hat{q}\sin\theta \]
LC振荡电路及其量子化
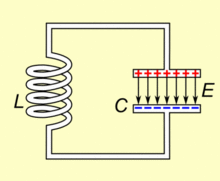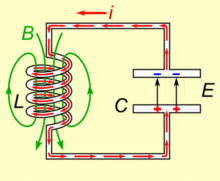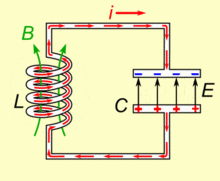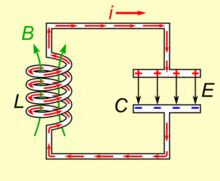
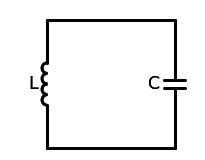
系统的哈密顿量为 \[ H = {Q^2\over2C}+{\Phi^2\over2L} \] 其中\(Q\)是电容的电荷量,\(\Phi\)是电感的磁通量 使用基本电荷\(e\)和磁通量子\(\Phi_0={h\over2e}\)改写,\(n={Q\over2e}, ~\phi={2\pi\Phi\over\Phi_0}={4\pi e\Phi\over h}\)可以有 \[ H = 4{e^2\over2C}n^2+{(\Phi_0/2\pi)^2\over2L}\phi^2 \] 可以进一步得到 \[ E_C = {e^2\over2C}~~~~E_L={(\Phi_0/2\pi)^2\over2L} \] 分别代表一个电荷所带来的电容器上的能量,以及一个磁通量子所带来的电感上的能量 量子化后有 \[ H=4E_C\hat{n}^2+E_L\hat{\phi}^2 \]
\[ [\hat \phi, \hat n]=i \]
约瑟夫森结
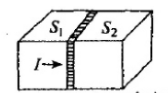
约瑟夫森结由两层超导体夹着一层绝缘体组成,其行为由约瑟夫森方程决定: \[ V(t)={\mathrm{d}\Phi(t)\over\mathrm{d}t} \]
\[ I(t)=I_s\sin(2\pi{\Phi(t)\over\Phi_0}) \]
其中,\(\Phi\)是以磁通量子为单位来描述的两超导体之间的序参量位相差
直流伏安特性
当偏置电流从0开始增大,结两端的电压一直为0,直到电流大于临界电流\(I_s\),此时结两端突然出现电压\(V=2\Delta/e\),其中\(\Delta\)是材料的超导能隙;继续增大电流,系统表现出正常电阻状态;减小偏置电压至\(2\Delta/e\),结两端电流减小至\(I_s\);电压继续减小,电流一直保持在\(I_s\),直到电压减小为0。
等效电感
\[ L = {V\over\dot I}={\Phi_0\over2\pi I_s\cos(2\pi{\Phi(t)\over\Phi_0})} \]
可以看到,对于一个约瑟夫森结,可以等效的看作有一个非线性的电感存在。 其包含的能量可以计算为 \[ E = \int IV\mathrm dt = {I_s\Phi_0\over2\pi}\int\sin(2\pi{\Phi(t)\over\Phi_0}){\mathrm{d}\Phi(t)\over\mathrm{d}t}\mathrm dt=-{I_s\Phi_0\over2\pi}\cos(2\pi{\Phi(t)\over\Phi_0}) \] 有 \[ E_J = {I_s\Phi_0\over2\pi} \] 表示一个磁通量子在约瑟夫森结中所带来的能量,考虑到和电荷能的对偶关系,可以认为是一对电子(一个库伯对)穿越约瑟夫森结时所需的能量 考虑仅含一个约瑟夫森结的闭合回路,由于结自身所带的电容\(C\),这构成了一个LC振荡电路,我们依据之前的关系,可以得到 \[ H = 4E_C\hat{n}^2-E_J\cos(2\pi{\hat\Phi(t)\over\Phi_0})=4E_C\hat{n}^2-E_J\cos\hat\phi \]
DC-SQUID
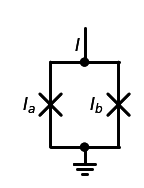
依照约瑟夫森结方程 \[ I=I_a\sin\phi_a+I_b\sin\phi_b \] 考虑a结和b结相同,则有 \[ \begin{align*} I &= I_a(\sin\phi_a+\sin\phi_b)\\ &= 2I_a\cos({\phi_a-\phi_b\over2})\sin({\phi_a+\phi_b\over2})\\ &= I_c\sin(\phi) \end{align*}\\ \] 考虑环形回路中有偏置磁通量\(\Phi_c\) 由\(\hbar\nabla\psi=2e\vec{A}\)有: \[ \begin{align*} \int_{SQUID}\hbar\nabla\phi\cdot\mathrm d\vec l = \int_{SQUID}2e\vec A\cdot\mathrm d\vec l\\ \Longrightarrow\hbar(\phi_a-\phi_b)=2e\cdot\Phi_c \end{align*} \] 由此我们得到: \[ I_c=2I_a\cos({2e\cdot\Phi_c\over2\hbar})=2I_a\cos(\pi\cdot{2e\over h}\cdot\Phi_c)=2I_a\cos(\pi{\Phi_c\over\Phi_0}) \] 最终,DC-SQUID和一个电容形成的超导回路,满足 \[ \begin{align*} H=4E_c\hat n^2-2E_{J, c}\cos\hat \phi\\ E_{J, c}=E_J\cos(\pi\cdot{\Phi_c\over\Phi_0}) \end{align*} \] 所以,如果我们调控偏置磁通量\(\Phi_c\),就能够人为的调控等效约瑟夫森结的电流\(I_c\),也就能调控\(E_{J, c}\),进而可以调控比特频率
Qubit Architecture
CPB(Cooper Pair Box)
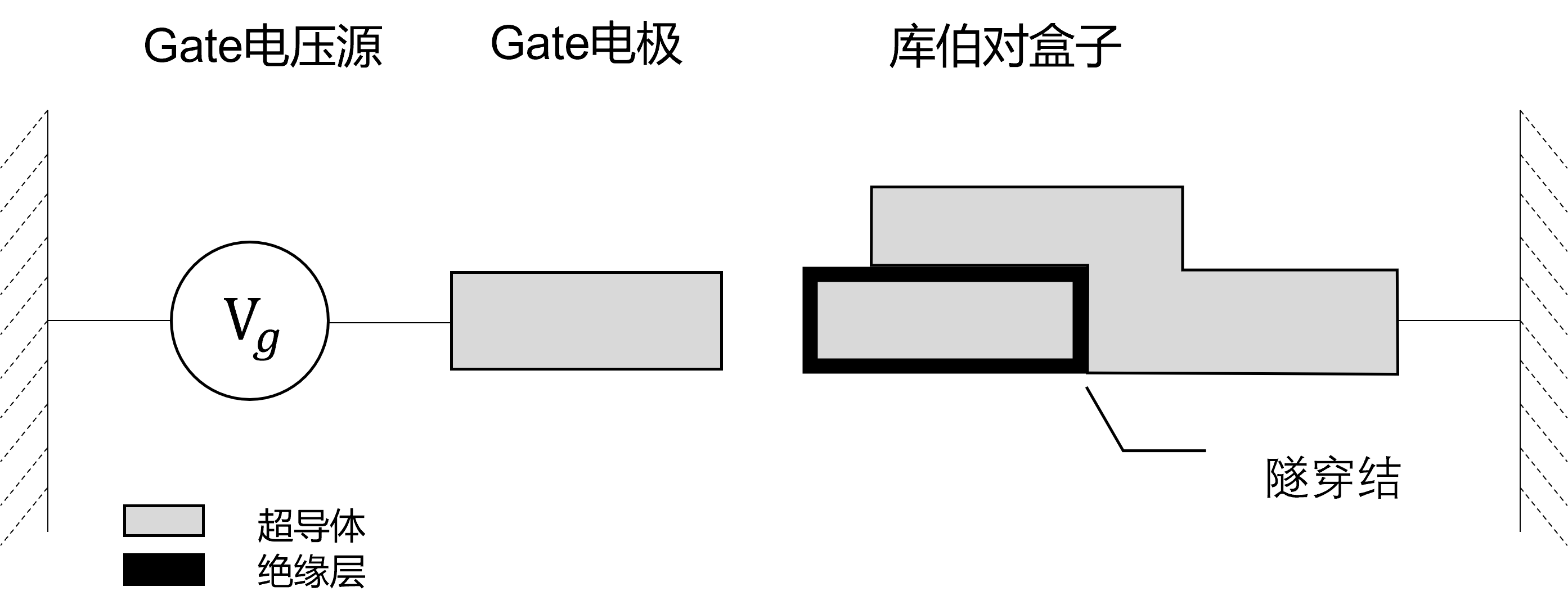
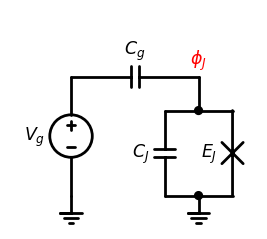
系统的广义动能项为 \[ T={C_g\over2}\dot\phi_J^2+{C_J\over2}\dot\phi_J^2={C_\Sigma\over2}\dot\phi_J^2 \] 其中\(C_\Sigma=C_g+C_J\)表征系统的总体电容值,代表了CPB的电荷储能能力以及系统量子态对电荷的敏感程度 CPB的广义势能项包括两个部分,约瑟夫森结的等效电感储能以及外部给予的电势能 \[ U = -E_J\cos({2\pi\over\Phi_0}\phi_J)-V_gC_g\dot\phi_J \] 可以得到CPB的哈密顿量为 \[ H = {(Q_J-C_gV_g)^2\over2C_\Sigma}-E_J\cos({2\pi\over\Phi_0}\phi_J) \]
Capacitive-shunted CPB
出于压制电荷噪声的考虑,可以提高CPB中的\(C_\Sigma\),因此加上一个旁接在结上的大电容\(C_{sh}\)。
满足条件\(C_{sh}\gg C_J\)
Cavity QED
重要的数学前提
\[ [a^\dagger, a]=-1 \]
\[ \sigma_z=\left[\begin{matrix}1 & 0\\ 0 & -1\end{matrix}\right]~~~~ \sigma_x=\left[\begin{matrix}0 & 1\\ 1 & 0\end{matrix}\right]~~~~ \sigma_y=\left[\begin{matrix}0 & - i\\ i & 0\end{matrix}\right] \]
\[ \sigma^+=\left[\begin{matrix}0 & 1\\ 0 & 0\end{matrix}\right]~~~~ \sigma^-=\left[\begin{matrix}0 & 0\\ 1 & 0\end{matrix}\right]~~~~ \] \[ \left[\sigma_i, \sigma_j\right]=2i\sigma_k~~~~\left[\sigma_z, \sigma^\pm\right]=\pm2\sigma^\pm \]
对易子运算关系 \[ [\hat A, \hat B] = -[\hat B, \hat A] \] \[ [\hat A, \hat B\hat C] = \hat B[\hat A, \hat C]+[\hat A, \hat B]\hat C~~~~~~~~ [\hat A\hat B, \hat C] = \hat A[\hat B, \hat C]+[\hat A, \hat C]\hat B \] 对易子是线性的 \[ [\hat A, \lambda\hat B+\hat C] = \lambda[\hat A, \hat B]+[\hat A, \hat C] \]
重要运算公式( BCS 展开公式) \[ e^{xA}Be^{-xA}=\sum_{n=0}^\infty\frac{1}{n!}x^nC_n \] 其中 \[ C_0=B~~~~C_n=[A, C_{n-1}] \]
表象变换
Picture 1 \[ i\hbar\dot{\ket{\psi}}=H\ket{\psi} \] Picture 2 \[ i\hbar\dot{\ket{\psi'}}=H'\ket{\psi'} \] P1 to P2 : \(\ket{\psi'}=U^\dagger\ket\psi\) \[ i\hbar\dot{\ket{\psi'}}=i\hbar\dot{U^\dagger}(U\ket{\psi'})+ U^\dagger[H(U\ket\psi')]=(i\hbar\dot{U^\dagger}U+U^\dagger HU)\ket{\psi'}\\ H'=U^\dagger HU+i\hbar\dot{U^\dagger}U \]
SW 变换
对于一阶非简并微扰系统 \[ H = H_0 + \lambda H_I\\ H\phi=E\phi \] 选取表象变换 \[ \psi=e^{\lambda S}\phi \] 可以得到 \[ \begin{align*} H_S &= e^{\lambda S}He^{-\lambda S}\\ &=H+[\lambda S, H]+\frac1{2!}[\lambda S, [\lambda S, H]]+\frac1{3!}[\lambda S, [\lambda S, [\lambda S, H]]]+\cdots\\ &=H_0+\lambda(H_I+[S, H_0])+\frac12\lambda^2(2[S, H_I]+[S, [S, H_0]])+O(\lambda^3) \end{align*} \] 选取 \[ H_I+[S, H_0]=0 \] 保留到二阶,有 \[ H_S=H_0+\frac12\lambda^2[S, H_I] \] 对于 \(H_0\) 的本征态 \(\ket m, \ket n\) \[ \begin{align*} &\bra m H_I\ket n + \bra m [S, H_0]\ket n =0\\ &\bra m H_I\ket n + \bra m SH_0-H_0S\ket n =0\\ &\bra m H_I\ket n + E_n\bra m S\ket n-E_m\bra mS\ket n =0\\ &\bra mS\ket n = \frac{\bra m H_I\ket n}{E_m-E_n} \end{align*} \] 由此,SW 酉变换的生成元算符 S 为 \[ S = \sum_{m, n}\frac{\bra m H_I\ket n}{E_m-E_n}\ket m\bra n \]
JC Model
\[ H=\hbar\omega_r(a^\dagger a+{1\over2})+{\hbar\Omega\over2}\sigma_Z+\hbar g(a\sigma^\dagger+a^\dagger\sigma^-)+H_\kappa+H_\gamma \]
其中,\(H_\kappa\)是腔的弛豫,\(H_\gamma\)是比特的弛豫
我们考虑旋转表象,对应的变换矩阵满足: \[ \ket{\psi_{rot}}=e^{ia^\dagger a\omega_rt+i\frac{\sigma_z}{2}\omega_qt}\ket{\psi_{Lab}}\\ U^\dagger=e^{ia^\dagger a\omega_rt+i\frac{\sigma_z}{2}\omega_qt}=e^{iH_0t/\hbar} \] 变换之后的哈密顿量为 \[ \begin{align*} H_{rot}&=U^\dagger HU+i\hbar\dot{U^\dagger}U\\ &=U^\dagger(H_0+V)U-H_0\\ &=U^\dagger VU\\ &=\hbar gU^\dagger(a^\dagger\sigma^-+a\sigma^++a^\dagger\sigma^++a\sigma^-)U \end{align*} \] 单独计算四项相互作用项有 \[ \begin{align*} &U^\dagger a^\dagger\sigma^-U=e^{ia^\dagger a\omega_rt+i\frac{\sigma_z}{2}\omega_qt}a^\dagger\sigma^-e^{-ia^\dagger a\omega_rt-i\frac{\sigma_z}{2}\omega_qt}=a^\dagger\sigma^-e^{i(\omega_r-w_q)t}\\ &U^\dagger a\sigma^+U=e^{ia^\dagger a\omega_rt+i\frac{\sigma_z}{2}\omega_qt}a\sigma^+e^{-ia^\dagger a\omega_rt-i\frac{\sigma_z}{2}\omega_qt}=a\sigma^+e^{-i(\omega_r-w_q)t}\\ &U^\dagger a^\dagger\sigma^+U=e^{ia^\dagger a\omega_rt+i\frac{\sigma_z}{2}\omega_qt}a^\dagger\sigma^+e^{-ia^\dagger a\omega_rt-i\frac{\sigma_z}{2}\omega_qt}=a^\dagger\sigma^+e^{i(\omega_r+w_q)t}\\ &U^\dagger a\sigma^-U=e^{ia^\dagger a\omega_rt+i\frac{\sigma_z}{2}\omega_qt}a\sigma^-e^{-ia^\dagger a\omega_rt-i\frac{\sigma_z}{2}\omega_qt}=a\sigma^-e^{i(\omega_r+w_q)t} \end{align*} \] 故此,哈密顿量可以分成两部分,高频部分和低频部分 \[ H_{rot} = \hbar g[(a^\dagger\sigma^-e^{i(\omega_r-w_q)t}+a\sigma^+e^{-i(\omega_r-w_q)t})+(a^\dagger\sigma^+e^{i(\omega_r+w_q)t}+a\sigma^-e^{i(\omega_r+w_q)t})] \] 一般来说 \(\omega_r\sim\omega_q\),对比前一项的低频项来说,后面的高频可以直接忽略掉吗,这称之为RWA(旋波近似)。
回到原来表象下的哈密顿量,可以简化为 \[ H = \hbar\omega_r(a^\dagger a+\frac12)+\frac12\hbar\omega_q\sigma_z+\hbar g(a^\dagger\sigma^-+a\sigma^+) \] 考虑到耦合项的形式,只有 \(\ket{n, g}\) 和 \(\ket{n-1, e}\) 耦合在一起,计算哈密顿量作用在非耦合态上的情况有 \[ \begin{align*} H\ket{0, g}&=-\frac12\hbar\Delta\ket{0, g}\\ H\ket{0, e}&=(\hbar\omega_r+\frac12\hbar\Delta)\ket{0, e}+\hbar g\ket{1, g}\\ H\ket{1, g}&=(\hbar\omega_r-\frac12\hbar\Delta)\ket{1, g}+\hbar g\ket{0, e}\\ H\ket{n-1, e}&=(n\hbar\omega_r+\frac12\hbar\Delta)\ket{n-1, e}+\hbar\sqrt{n}g\ket{n, g}\\ H\ket{n, g}&=(n\hbar\omega_r-\frac12\hbar\Delta)\ket{n, g}+\hbar \sqrt{n}g\ket{n-1, e} \end{align*} \] 其中,\(\Delta=\omega_q-\omega_r\) 表示人工原子和腔之间的失谐,可以发现,除了基态外,其余各态都出现了临近态耦合的情况,也即哈密顿量分块对角。 \[ H_n=\left[\begin{matrix}n\hbar\omega_r+\frac12\hbar\Delta & \sqrt{n}\hbar g\\\sqrt{n}\hbar g & n\hbar\omega_r-\frac12\hbar\Delta\end{matrix}\right] \]
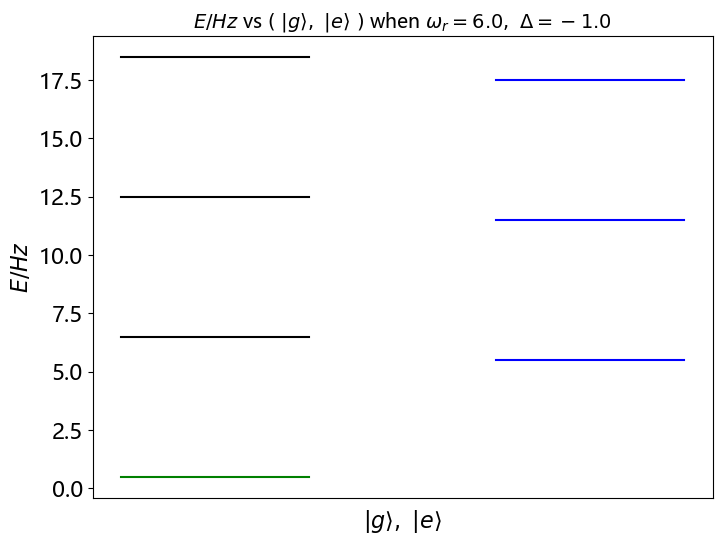
可以求解出系统的能级和本征态(在这个系统中这里又可以称为缀饰态) \[ E_0=-\frac12\hbar\Delta\\ E_{n, \pm}=n\hbar\omega_r\pm\frac\hbar2\sqrt{4ng^2+\Delta^2} \]
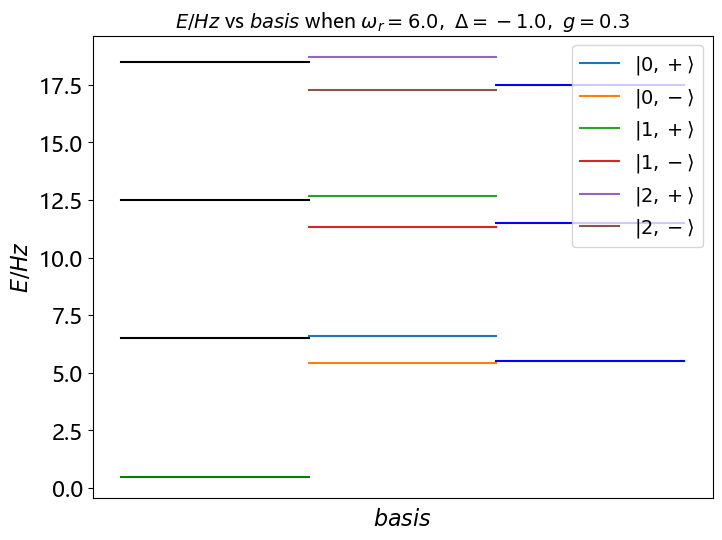
\[ \begin{align*} \ket{0}&=\ket{0, g}\\ \ket{n, +}&=\cos\theta_n\ket{n, g}+\sin\theta_n\ket{n-1, e}\\ \ket{n, -}&=-\sin\theta_n\ket{n, g}+\cos\theta_n\ket{n-1, e}\\ \theta_n&=\frac12\arctan{\frac{2\sqrt{n}g}{|{\Delta}|}} \end{align*} \]
注意,这里考虑的是 \(\Delta<0\) ,另一边的情况下,形式有所不同,但最终的结果是自洽的,也因此后续采用SW变换来得到最终结果,更为直接简洁。
考虑色散区(大失谐条件 \(g\ll|\Delta|\) ) \[ \begin{align*} E_{n, \pm}&=n\hbar\omega_r\pm\frac\hbar2|\Delta|\sqrt{1+4n\frac{g^2}{\Delta^2}}\\ &=n\hbar\omega_r\pm\frac\hbar2|\Delta|(1+2n\frac{g^2}{\Delta^2})\\ &=n\hbar(\omega_r\pm\frac{g^2}{|\Delta|})\mp\frac\hbar2|\Delta|\\ \end{align*} \]
\[ \ket{n, +}\simeq\ket{n, g}+\sqrt{n}\frac{g}{|\Delta|}\ket{n-1, e}\\ \ket{n, -}\simeq-\sqrt{n}\frac{g}{|\Delta|}\ket{n, g}+\ket{n-1, e} \]
在低能级的情况下,\(\frac{g}{|\Delta|}\ll1\) 的近似条件是合理的,但是在 n 比较大的情况下,小量近似将不再成立,更强的近似条件其实是 \(\frac{2\sqrt{n}g}{|\Delta|}\ll1\)
如果我们考虑 \[ \ket{n, +}\simeq\ket{n, g}\\ \ket{n, -}\simeq\ket{n-1, e} \] 那么哈密顿量可以近似写为 \[ \begin{align*} H &= E_0\ket{0, g}\bra{0, g}+\sum_{n=1}^{\infty}(E_{n, +}\ket{n, +}\bra{n, +}+E_{n, -}\ket{n, -}\bra{n, -})\\ &=-\frac12\hbar\Delta\ket{0, g}\bra{0, g}+\sum_{n=0}^{\infty}n\hbar\omega_r\ket n\bra nI_q+\sum_{n=0}^{\infty}n\hbar\frac{g^2}{\Delta}\ket n\bra n\sigma_z\\ &~~~~~+\frac12\hbar\Delta\ket{0, g}\bra{0, g}+\sum_{n=0}^{\infty}\hbar(\omega_r+\frac{g^2}{\Delta})\ket n\bra n~\ket e\bra e+\frac12\hbar\Delta\sum_{n=0}^{\infty}\ket n\bra n\sigma_z\\ &=\hbar\omega_ra^\dagger a+\hbar\frac{g^2}{\Delta}a^\dagger a\sigma_z+\frac12\hbar\Delta\sigma_z+\hbar(\omega_r+\frac{g^2}\Delta)\ket e\bra e \end{align*} \] 考虑到 \[ \hbar(\omega_r+\frac{g^2}\Delta)\ket e\bra e=\frac\hbar2(\omega_r+\frac{g^2}\Delta)\sigma_z+\frac\hbar2(\omega_r+\frac{g^2}\Delta)I_q \] 由此哈密顿量可以简化为 \[ \begin{align*} H &=\hbar\omega_ra^\dagger a+\hbar\frac{g^2}{\Delta}a^\dagger a\sigma_z+\frac\hbar2(\Delta+\omega_r+\frac{g^2}\Delta)\sigma_z\\ &=\hbar(\omega_r+\frac{g^2}{\Delta}\sigma_z)a^\dagger a+\frac\hbar2(\omega_q+\frac{g^2}\Delta)\sigma_z \end{align*} \]
JC Model 的 SW 变换
\[ H = \hbar\omega_r(a^\dagger a+\frac12)+\frac12\hbar\omega_q\sigma_z+\hbar g(a^\dagger\sigma^-+a\sigma^+) \]
先考虑相互作用绘景的表象变换 \[ U^\dagger=e^{i\omega_ra^\dagger at+i\omega_r\sigma_zt} \] 将 JC 哈密顿量分解为两部分 \[ H_0 = \hbar\omega_r(a^\dagger a+\frac12)+\frac12\hbar\omega_r\sigma_z\\ H'=\frac12\hbar\Delta\sigma_z+\hbar g(a^\dagger\sigma^-+a\sigma^+) \] 变换得到 \[ U^\dagger HU=H' \] 选取生成元算符 S \[ S = \sum_{m, n}\frac{\bra m H_I\ket n}{E_m-E_n}\ket m\bra n\\ 其中~m=e, g; n=e, g\\ H_I=\hbar g(a^\dagger\sigma^-+a\sigma^+)\\ H'=H_0'+H_I \] 可以得到 \[ \begin{align*} S &= g\frac{\bra e a^\dagger\sigma^-+a\sigma^+\ket g}{\Delta}\ket e\bra g+g\frac{\bra g a^\dagger\sigma^-+a\sigma^+\ket e}{-\Delta}\ket g\bra e\\ &=\frac{g}{\Delta}(a\ket e\bra g-a^\dagger\ket g\bra e)\\ &=\frac{g}{\Delta}(a\sigma^+-a^\dagger\sigma^-) \end{align*} \] 根据 SW 变换有 \[ H'=\frac12\hbar\Delta\sigma_z+\frac12[S, H_I] \] 其中 \[ \begin{align*} [S, H_I]&=[\frac g\Delta(a\sigma^+-a^\dagger\sigma^-), \hbar g(a\sigma^++a^\dagger\sigma^-)]\\ &=2\hbar\frac{g^2}{\Delta}[a\sigma^+, a^\dagger\sigma^-]\\ &=2\hbar\frac{g^2}{\Delta}(a^\dagger a\sigma_z+\frac12+\frac12\sigma_z) \end{align*} \] 最终有 \[ H' = \frac12\hbar(\Delta+\hbar\frac{g^2}{\Delta})\sigma_z+\hbar\frac{g^2}{\Delta}a^\dagger a\sigma_z+\hbar\frac{g^2}{\Delta} \] 回到原表象可以得到 \[ H = \hbar(\omega_r+\frac{g^2}{\Delta}\sigma_z)(a^\dagger a+\frac12)+\frac\hbar2(\omega_q+\frac{g^2}{\Delta})\sigma_z \]